Escales amb volta a la catalana Estudi d’una escala tipus de qualsevol edifici d’habitatges de principis de segle XX

Com treballen les voltes i els arcs

Més d’una vegada, tot visitant algun edifici romànic, gòtic o fins i tot d’arquitectura modernista com ara els magnífics cellers del Priorat, hem escoltat explicacions referents a les principals característiques arquitectòniques i estructurals dels elements que els conformen, normalment sense entrar massa en detalls. Es diu que cal adonar-se que tots els elements que es poden veure són estructurals i que tots treballen només a compressió: els murs, els contraforts, els arcs volants, les arcades, les voltes, els nervis dels creuers, etc. S’acostuma a ponderar precisament l’enginy de mestres d’obra i arquitectes, que consistia en aconseguir grans dimensions, grans espais i llum d’obra, a base de fer treballar tots els elements només a compressió. De vegades s’explica algunes nocions de grafostàtica per fer més entenedor com s’arribava a conèixer les sol·licitacions i fins i tot com a eina per a dimensionar la forma concreta d’alguns arcs o d’altres elements.

Caldria matisar aquestes afirmacions. Certament que en aquest tipus d’edificis tots els elements són estructurals, però el que no és tan cert és que treballin “només a compressió”. La realitat és que tots treballen a flexocompressió. És a dir, considerant la linealitat estructural d’un arc o d’una volta, la secció al llarg de tota la longitud de l’element que conforma l’estructura de l’arc, resta afectada per uns determinats moments flectors (positius o negatius), per unes sol·licitacions normals (axials) i evidentment per uns esforços tallants.

El que passa però, és que l’esforç normal (axial) genera unes tensions de compressió molt importants. Però de sol·licitacions, n’hi ha d’altres a més de l’esforç de compressió. Per entendre’ns: si comparàvem un arc (línia corba convexa) amb una biga (lineal recta), veuríem que la incidència de la sol·licitud normal (axial) en el cas de l’arc té una importància enorme en la consecució de l’equilibri i estabilitat, mentre que en el cas de les bigues (armat passiu), aquest tipus de sol·licitud acostuma a afectar molt poc l’estabilitat del sistema. Sí que podríem establir una similitud en aquest sentit (importància de les tensions normals), entre els arcs i les bigues pretesades en què els esforços de pretesat o posttesat hi juguen un paper essencial.

Vegem-ho de forma més gràfica. A la Fig.1, es mostra un arc rebaixat, carpanell, de dos radis, amb el corresponent diagrama de moments i l’anotació del valor dels moments i axials de càlcul dels punts més significatius. Li apliquem una càrrega corresponent a pes mort, G=1.5 T/m. L’arc, a efectes de càlcul, se l’ha modelitzat per segments rectes i nusos rígids. Per simular els contraforts, els nusos que conformen el pilars, tenen impedit el desplaçament en sentit horitzontal.

Fàcilment es veu la distribució de moments, positius a la zona central de l’arc, i negatius a banda i banda (els “ronyons”), passant per un punt de moment Md =0.00 mT. Es pot observar con l’esforç normal (axial) és important tot al llarg del desenvolupament de l’arc i que té un valor significativament elevat (8.90 T<11.50 T).><Nd<11.50T).

Si consideràvem les seccions com si només estiguessin afectades per les sol· licituds dels moments flectors, veuríem que les fibres extremes de cada secció que consideréssim, treballarien segons els casos a tracció o a compressió. En les zones de moment negatiu, la fibra superior a tracció i la inferior a compressió i a les zones de moment positiu, a l’inrevés.

Ara bé, com deia, cal tenir en compte la incidència de l’esforç axial, que comprimeix més encara les fibres comprimides per l’acció del moment flector, i fa minvar (o neutralitza segons els casos) la tracció de les fibres traccionades. Però aquesta “compensació”, a les fibres més traccionades, no sempre neutralitza les traccions del tot, cosa que fa que en determinades seccions (les de moment flector més elevat) hi pugui haver fibres extremes que treballin només a tracció.

Vegem-ho en la Fig.2, corresponent a la secció més desfavorable de la zona lateral (els “ronyons”) de l’arc rebaixat.

Sabem que les sol·licituds de càlcul són les següents: Md=-2.85 mT, Nd=-11.46 T. Hem fet un primer dimensionat de la secció (bh) de 45*45 cm2 per veure com es comportaria l’arc en la zona més desfavorable.

El mòdul resistent elàstic serà, per tant:

I la tensió a les fibres extremes originada només pel momento flector:

Si ara considerem a banda la repercussió de l’esforç axial, que se suma a les tensions originades pel moment flector, tindrem:

Per tant, finalment, la fibra més comprimida treballarà:

i la fibra menys comprimida treballarà

és a dir, treballarà a tracció.

Si l’arc fos de formigó armat, no hi hauria cap problema amb aquesta secció, perquè podríem absorbir les traccions de la cara superiors (als “ronyons”) o de la cara inferior a la zona central de l’arc, amb l’armadura corresponent. Però, ¿què passaria si l’arc fos de fàbrica de totxo massís, per exemple?: que a la zona dels ronyons, la part inferior estaria comprimida amb un tensió perfectament assumible per la fàbrica, però, la part superior estaria (potser) excessivament traccionada i per tant (potser) s’esquerdaria. Això ens duria a estudiar la possibilitat de resoldre l’arc amb una secció de mòdul flector elàstic (Wx) de valor superior que ens assegurés que totes les fibres estiguessin comprimides, o bé traccionades amb una tensió assumible per la fàbrica de totxo massís.

Aquí sorgeix la pregunta “del milió”: ¿A quant pot treballar a tracció la fàbrica ceràmica?, perquè resulta que en comprovar les sol·licitacions de la majoria d’arcs i voltes dels edificis que coneixem, ens trobem, amb gran sorpresa, que hi ha moltes seccions d’obra de fàbrica, amb fibres extremes traccionades, amb tensions de certa importància, i el més curiós és que en la majoria dels casos no hi ha cap mena de fissura ni d’esquerda, la qual cosa vol dir que la fàbrica ceràmica pot treballar relativament bé a tracció, força més enllà del quilo-quilo i mig o dos quilos per centímetre quadrat que els tècnics acostumen a tenir al cap. En el cas que tot seguit desenvoluparem, el de les voltes a la catalana que tan satisfactòriament s’han comportat fins ara, això és més que evident.

Les voltes a la catalana

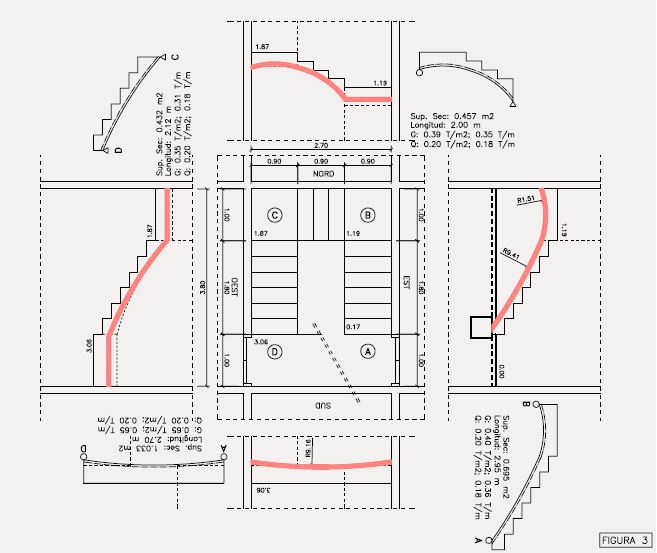
Proposo l’estudi d’una escala “tipus” que podríem trobar a qualsevol edifici d’habitatges de principis de segle XX, Fig. 3. Aquestes voltes es resolien normalment amb un desenvolupament corbat, de dos radis als trams ascendents/descendents, i d’un radi als replans d’accés als habitatges. Evidentment, hi ha moltes variables pel que fa a solucions fetes a base d’aquesta tecnologia que vàrem heretar dels romans. Em refereixo a la formació de petxines i altres “moviments” per evitar arestes, etc.

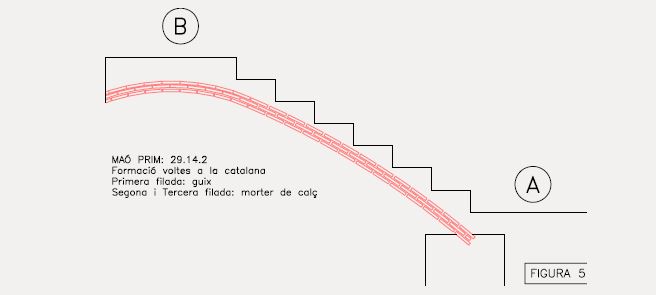
Centrem-nos en aquest tram ascendent B-A (Fig 4).

Té dos radis de curvatura, el superior, a tocar el replà, R1 =1.55m i el de la llosa ascendent R2 =9.41m. Observem el diagrama de moments. Hi ha una sector amb moments negatius i un altre amb moments positius. El més desfavorable correspon a un punt del tram de radi R2 , és a dir el de menys curvature.

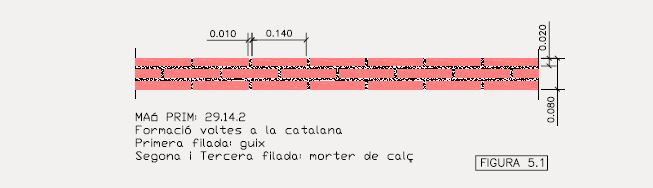
La secció de la volta és la “típica”, a base de tres capes de maó massís de 20 mm de gruix. El que se’n diu, volta de maó de pla de tres gruixos. (Fig 5 i 5.1) Com se sap, la tècnica dels paletes evitava la necessitat d’emprar bastides. Collaven la primera capa amb pasta de guix, disposant els maons a trencajunt, seguint el replanteig de la corba que havien replantejat a la paret, ajudant-se d’una mestre de guix que els servia per situar el primer maó arran de paret. Les altres dues capes les acostumaven a collar amb morter de calç, damunt de la capa inferior, i sempre a trenca junt en els dos sentits per tal que tot plegat restés ben travat. La secció acostumava a tenir un gruix de 8 cm i l’amplada, en funció del previst a projecte. En el cas que proposem, de 90 cm.

Observem també l’estat de càrregues: les càrregues mortes (G=0.35 T/m) son el 66% de les càrregues totals (Q=0.18 T/m). Això vol dir, que quan el paleta feia l’escala i acabava l’esglaonament, la volta tenia la càrrega permanent suficient com per a verificar que l’obra havia estat ben resolta. Si no hagués estat així, la volta s’hauria esberlat gairebé immediatament, esquerdant-se per la part més feble i/o més tensionada.

Tornem a fer els “números” que hem fet abans considerant l’arc rebaixat, per veure com anem de “tensions” a la nostra volta a la catalana.

Mòdul resistent elàstic de la secció:

Moment flector màxim: Md=+0.13 mT

Axial: Nd=-3.36 T

Tensions (de càlcul):

Operant, arribem a la conclusió que la fibra més comprimida (en aquest cas, superior de la volta) està treballant a una tensió en principi assumible per la fàbrica: σd.sup=-18.21 K/cm2 , una compressió “raonable”. Però la fibra inferior, està treballant a una tracció de càlcul notable: σd.inf=+8.88 K/cm2 . En aquesta situació, a primer cop d’ull, hauríem de dir que aquesta volta no aguanta, que amb aquesta tensió a tracció segur que la fàbrica de maó s’esquerdaria. Doncs bé, si això fos així la majoria de voltes de les nostres escales estarien enrunades a hores d’ara. Ni existirien. Però tots sabem que això no és així. Fins i tot s’han fet proves de càrrega per veure fins a on aguantaven, a base de moltes capes de sacs de sorra, i les voltes se seguien aguantant.

Fixem-nos ara en el tram del replà, D-A. (Fig 6) d’un sol radi de curvatura (R=9.16 m).

Fent els mateixos “números” que hem fet abans, veuríem que la secció més desfavorable és la zona central, amb un moment positiu Md=+0.58 mT, i un esforç normal de Nd=-12,70 T. La secció és de 100*8 cm2 , i el mòdul resistent elàstic, Wx =1067 cm3 . La fibra més comprimida és la superior i té una tensió σd.sup=-70.28 K/cm2 , i una tensió de tracció a la fibra menys comprimida, la inferior σd.inf=+38.48 K/cm2 . Evidentment, aquesta llosa del replà, amb aquestes tensions s’hauria esquerdat pel mig marcant la fissura a tota la secció. Però, possiblement, la llosa seguiria aguantant-se. Ho anirem veient.

Suposem doncs que la nostra volta efectivament marca una esquerda. Arribem a la conclusió que el que havia estat un “sistema lineal”, ha format al punt de màxima tensió una ròtula (plàstica), que ha originat una nova distribució de sol·licitacions (moments, axials) en el sistema. Com si fossin dues “bigues” que als extrems, es recolzen a les parets, i una en l’altre al mig del replà. Aquesta “ròtula” i punt de recolzament, hauria d’absorbir i fer-se càrrec del “nou” esforç normal i del tallant, però ja no de cap moment, perquè el moment en aquest punt seria “zero” com pertoca a un recolzament articulat. Es pot veure la nova distribució de moments a la Fig 6. Concretament l’esforç axial en el punt en què s’hauria format la ròtula (esquerda) seria de Nd=- 19.08 T. Atès que la fractura s’hauria fet a tota la secció, podríem considerar que tota ella absorbiria la sol·licitació axial, i que per tant la tensió (unitària) seria:

una tensió assumible per la fàbrica a compressió, raó per la qual, aquesta volta amb una esquerda transversal “encara” s’aguantaria. Si no fos així, el més probable és que al cap de poc temps de la seva construcció, s’hauria esfondrat. En tot cas, si encara ens la trobàvem “en servei” en alguna revisió tècnica, caldria seguir verificant les tensions de les seccions més desfavorables en aquest nou estat estructural “no lineal”.

Suposem, que una altra secció de la mateixa volta també es fracturés. Tindríem en conjunt un element no lineal amb dues ròtules sempre i quant les tensions fossin assumibles per la secció de fàbrica. Encara podria ser estable si les tensions no fossin excessives. Si es produïa una nova “ròtula” aleshores el sistema fóra un “mecanisme” i esdevindria totalment inestable: s’esfondraria segur (o s’hauria esfondrat ja). Desenvolupar ara aquest punt ens duria molt més enllà de l’article. Cal tenir present doncs aquest aspecte com a criteri tècnic si mai havíem de fer algun estudi d’elements en arc o volta esquerdats per tal d’evitar falses alarmes. Cal pensar que la majoria d’aquestes esquerdes s’han produït molt temps enrere i que l’escala o la volta encara s’aguanta.

Pel que fa doncs a aquest replà, el tram D-A de l’escala, hauria estat més ben resolt al seu dia, amb volta de pla de quatre gruixos enlloc de tres, i per tant un gruix total de secció d’onze centímetres en lloc de vuit. Aleshores el mòdul resistent elàstic de la secció s’hauria incrementat gairebé al doble, Wx =2017 cm3 , i en conseqüència, les tensions màximes haurien estat σd.sup=-40.32 K/cm2 i σd.inf=+17.20 K/cm2 . Molt probablement, no hi hauríem vist cap esquerda malgrat que les tensions fossin importants. Si nosaltres al seu dia, haguéssim hagut de dimensionar aquest arc, hauríem estudiat millor el radi de curvatura i el gruix de la secció abans de fer l’obra.

Els resultats del conjunt dels trams de l’escala es resumeixen en la Taula 1. Podem constatar les diverses tensions (de càlcul), tant a tracció (positives) com a compressió (negatives), i constatar que les traccions a la columna de “fibra menys comprimida” no es poden menystenir. Més endavant reprendrem el tema per veure com aniríem pel que fa a la seguretat del sistema, tal i com es pot veure a les columnes de la taula (γf ) considerant per separat les fibres extremes de cada secció.

Com treballa la fàbrica ceràmica a tracció

Hem vist doncs, que un arc carpanell i unes voltes d’escala, tenen trams sol·licitats per esforços de tracció. I ací ens hem de preguntar, com treballa la fàbrica ceràmica a tracció. Com deia abans, aquesta és la pregunta del milió. El CTE-SE-F 4.6.4 contempla només dues hipòtesis pel que fa a les traccions originades per la flexió que actua a les parets de fàbrica segons el pla de ruptura sigui paral·lel a les esteses, o bé perpendicular (Fig. 7). És a dir, quan apareixen esquerdes horitzontals o verticals causades per una tracció a causa d’algun moment flector, normalment per guerxament o a causa de deformacions estructurals o també pel vent. A la taula 4.6, segons els tipus de morter i de peces ceràmiques o de formigó, el CTE proposa uns valors característics concrets compresos entre fk=0.05 N/mm2 , fins a fk=0.4 N/mm2 , en funció de la qualitat dels materials.

A finals de l’any 2006 es va publicar un article que resumia i seguia treballant en la línia de la tesi doctoral (2004) del Dr. E. Reyes de la UPM. L’article està firmat pel susdit enginyer i altres professors de la UPM i de la U. de Castilla. Es titula “Estudio experimental de la fisura de la fábrica de ladrillo bajo solicitaciones de tracción y cortante en modelos reducidos”. A la Fig. 8 es pot veure en esquema, el tipus de provetes a partir de les quals es va fer la campanya d’assaigs. Tot es va treballar a escala respecte a les dimensions de l’obra de fàbrica real, la qual cosa els va permetre de treballar amb òptimes condicions a laboratori i disposar d’una bona “població” per analitzar des del punt de vista estadístic el comportament de la fàbrica.

El que es va poder verificar és com treballa l’obra de fàbrica a tracció i a tallant (ara aquest aspecte ens interessa menys) segons diversos graus d’inclinació de les esteses de la fàbrica: 0º, 30º, 45º, 60º i 90º, i també el mòdul elàstic (tangencial) corresponent en cada cas. Els resultats potser eren d’esperar però en tot cas no deixen de ser sorprenents. Resulta que la fàbrica de ceràmica treballa a tracció molt millor del que hom hauria esperat i per descomptat del que “es deia”. La prova és que les nostres voltes d’escala a la catalana s’aguanten la mar de bé suportant unes tensions de tracció més que notables en molts casos. Recomano la lectura del susdit article. Adjunto ací la taula resum del treball d’investigació: (Taula 2).

Fixem-nos que si l’obra de fàbrica es considera d’estesa “horitzontal” (som en el cas de la volta de maó de pla de tres gruixos que conforma la majoria de voltes a la catalana de les escales dels nostres edificis d’habitatges de principis de segle XX) la tensió de ruptura a tracció és de σt =5.8 N/ mm2 . En canvi, si es tracta d’un element, sigui una volta o arc però a plec de llibre o sardinell, estem en el cas que es considera d’estesa “vertical”, aleshores la tensió de ruptura és només de σt =2.4 N/mm2 .

Els autors de l’article, a les conclusions, constaten “la forta dependència que tenen les propietats mecàniques de la fàbrica en funció de la orientació de les esteses, que actuen com a pla de debilitat” i també que “els resultats experimentats de ruptura de fàbrica sota sol·licitacions de tracció i tallant, mostra una reduïda dispersió experimental”. També comenten que “seria molt convenient comparar els resultats dels assaigs de fractura a escala amb assaigs a escala real, cosa que no és possible per manca de literatura”.

Seguretat estructural

Criteri probabilista

A l’hora d’avaluar la seguretat estructural en els estudis sobre edificis existents el problema que se’ns planteja és que ens hem de moure en l’àmbit probabilista i per tant hem d’aplicar coeficients parcials (γM) sobre els valors característics dels materials, però aquests coeficients parcials no estan definits a la normativa (ni són fàcils de definir). Efectivament, el CTE contempla la fase de projecte però no la fase de rehabilitació o de revisió tècnica. I quina diferència hi ha entre la fase de projecte i la fase d’edifici existent? que els nivells d’incertesa són molt diferents. Quan es projecta un edifici la incertesa que es vol assegurar amb els coeficients parcials fa referència bàsicament a la bondat i qualitat dels materials i a la bondat de l’execució i posada en obra. En canvi, en un edifici existent, aquestes incerteses no existeixen, perquè l’obra o l’element estructural és allà i en principi “s’aguanta” ni que s’hi observin patologies. I, pel que fa a la seguretat respecte a les accions, si “s’aguanta”, al menys li hauríem d’atribuir el coeficient γf =1.

Resistència a compressió

Referent a l’obra de fàbrica, el CTE-F, quan concreta el valor característic de resistència a compressió contempla l’acció de la força en sentit perpendicular a les esteses en funció del tipus de peça (fb), del morter (fm) i de les condicions d’execució (A,B,C). A l’annex C concreta les bases de càlcul que permeten d’arribar als resultats de la taula 4.4. Al punt 4.6.2.3 diu “cuando la solicitación sea paralela a los tendeles (cas de les voltes a la catalana) la resistencia característica a compresión, puede determinarse con el anejo C, adoptando como resistencia normalizada a compresión fb de la pieza la correspondiente a dicha dirección”. Però, com que no diu que sigui diferent a la de la direcció perpendicular, se suposa que deu ser la mateixa a no ser que es disposi d’assaigs de laboratori al respecte que puguin justificar un valor determinat.

Si apliquem la fórmula que proposa , i si considerem que una obra de fàbrica de totxo massís, collada amb morter de calç té els paràmetres: fb=10 N/mm2 , K=0.60 i fm=5 N/mm2 , aleshores la resistència característica será fk=4.01 N/mm2 ; o bé si considerem que: fb=15, K=0.60 i fm=7.5, la resistència característica a compressió serà fk= 5.77 N/mm2 . Adoptem, mancats de més informació, el darrer valor, amb les reserves que hom consideri oportú.

Ateses les consideracions formulades fins ara, podríem acceptar les resistències característiques que preconitza la norma, però aplicant un coeficient “d’obra existent” de valor inferior al que es preveu per a obres en “projecte”. La meva proposta, també totalment discutible, és d’adoptar γM=1.5. Això ens donaria una resistència de càlcul per a obra de fàbrica existent (massís+morter de calç).

Resistència a tracció

Tornem als arcs i les voltes. Considerant i acceptant com a correctes els resultats de la investigació feta a la UPM i UC (resistència de ruptura a tracció de la fàbrica segons la direcció de l’estesa), si mai ens interessava fer alguna verificació d’algun arc estructural de fàbrica, o d’alguna volta d’escala existents per límits últims, també hauríem d’aplicar a aquests resultats un coeficient parcial γM. Pel que fa a les sol·licitacions de tracció, i tenint en compte que es tractaria d’una obra existent, i que les dades de què partim, les de la investigació, es varen obtenir treballant amb provetes fetes a escala i en condiciones de laboratori, crec (és totalment discutible) que fóra una bona ponderació un coeficient γM=2.50, la qual ponderació ens duria a considerar una resistència de càlcul a tracció per a la fàbrica de les voltes a la catalana de

(fàbrica de pla) i

per als arcs i voltes a sardinell.

Seguretat a l’escala de la Figura 3

Si mirem la Taula 1, veurem que tots els trams tenen fibres traccionades amb tensions que van des de 2.55 k/cm2 (C-B) fins a 16.17 K/cm2 (D-C) deixant de banda el tram A-D que acabem de considerar més amunt. Estaríem treballant doncs amb un coeficient de seguretat sobre les accions en el cas més desfavorable de

Evidentment, la “nostra” volta a la catalana no hauria de manifestar cap senyal de trencament, ni fissura, ni cap patologia estructural malgrat que la secció més desfavorable estigués sotmesa a esforços de tracció importants.

Si fèiem la mateixa verificació en el cas de l’arc rebaixat (carpanell) (Fig 1) de què parlàvem en començar l’article, (recordem que la tensió de càlcul a la zona dels “ronyons” era σd.sup= +13.11 K/cm2 ) atès que era de fàbrica a sardinell, hauríem de considerar que la resistència de càlcul seria només fd=9.60 k/cm2 , i per tant, el coeficient de seguretat sobre les accions fóra:

El coeficient es podria considerar insuficient però l’obra de fàbrica probablement no presentaria cap fissura (no hauria arribat al límit de ruptura). Potser podríem donar la secció existent per bona, sempre i quan ens asseguréssim molt bé de l’estat de càrregues i potser programant revisions periòdiques. Altra cosa fóra si estiguéssim en fase de projecte: aleshores hauríem d’incrementar el dimensionat de la secció per millorar el coeficient de seguretat. Si l’arc hagués estat fet a base de filades de pla com és el cas de les voltes a la catalana, amb esteses a 0º respecte al sentit de les sol·licitacions de tracció, el coeficient hauria estat més que suficient, atès que la capacitat de treball de la fàbrica és superior.

Sembla doncs, que ja tenim resposta per a la pregunta del “milió” que ens fèiem més amunt. Ara sabem d’una manera plausible la raó del bon comportament de les voltes a la catalana, i també sabem que no és el mateix construir un arc de fàbrica a sardinell, que un arc construït amb diversos gruixos de maó pla, pel que fa a la seva capacitat resistent, si el que consideràvem és la tracció. La resposta és clara: la fàbrica de ceràmica segons l’orientació de les esteses respecte a les forces de tracció, pot tenir i de fet té, una gran capacitat de resistència. La manera de fer les voltes a la catalana, amb les esteses seguint la direcció de les sol·licituds de tracció, fa que s’optimitzi la possibilitat de tracció de la fàbrica ceràmica.

Adjunto un parell de fotos que corresponen a edificis prou coneguts de l’arquitecte català Cèsar Martinell. Concretament les grans arcades del Celler Cooperatiu de Gandesa, resolt amb fàbrica de pla de sis a deu capes de maó de 4 cm de gruix, i el Celler de Sant Cugat del Vallès (fotografia inferior), resolt a base de plec de llibre de secció mínima 30×45 cm, també amb maó de 4 cm arrodonit. Dues maneres de fer treballar la fàbrica ceràmica. La de Gandesa, més favorable pel que fa a resistir les traccions.

Patologies de les voltes a la catalana

Però aleshores sorgeix una altra pregunta: Per què si la fàbrica ceràmica de pla de diversos gruixos treballa força bé a tracció, de vegades apareixen esquerdes (sobretot transversals) a la part superior (es veuen menys) o inferior en alguns trams de voltes a la catalana a les escales? La resposta més adient cal cercar-la en el comportament de les parets que conformen la caixa de les escales. Sigui per la raó que sigui poden haver cedit sota la sol·licitud de recolzament (l’empenta) de les voltes. Les voltes per aquesta raó s’han obert. Per això molt sovint, apareixen esquerdes a les parets de les caixes d’escala i sovint, a la vora de les cantonades. La situació és més desfavorable com més amunt de l’edifici ens situem, atès que la component de càrrega vertical (pes propi de la paret més les càrregues provinents dels forjats) va minvant a mesura que anem pujant cap a coberta.

¿Com afecta aquest desplaçament a la volta de l’escala? Molt senzill: el desplaçament horitzontal fa minvar de sobte l’esforç “normal” axial que compensava les traccions originades pel moment flector, fent que a les fibres extremes -que ja estaven traccionades però dins de la “zona de seguretat”- s’incrementi significativament la tracció, arribant a la tensió de ruptura. L’esquerda que s’origina, trenca la linealitat del sistema i provoca la formació d’una ròtula amb la consegüent redistribució de moments fins arribar a l’equilibri del sistema un altre cop, o bé a la formació d’una segona ròtula, etc. com hem explicat més amunt.

El que cal doncs, és localitzar per on s’ha eixamplat la caixa d’escala i fixar-ne i impedir-ne l’expansió com sigui perquè el problema no vagi endavant fins al col·lapse. I en tot cas, modelitzar l’estructura amb les ròtules corresponents, coneixent la secció real de la volta, per tal de verificar l’estat tensional real i saber els nivells de seguretat de les voltes. Així doncs, de res serviria actuar sobre les voltes esquerdades si no s’actuava sobre les causa més plausible: l’eixamplament de la caixa d’escala.

És possible que hi hagi altres causes, com ara que la volta s’hagi fet només amb un doblat simple, o bé que s’hagin produït amb el temps deformacions plàstiques que hagin incrementat el radi de curvatura sobretot de la part més “plana” de la volta. Però aquestes “causes” haurien manifestat patologies ja al cap de cinc o sis anys de la construcció de l’edifici.

En alguna ocasió s’han produït patologies a causa de la instal·lació d’ascensors al nucli d’algunes escales, perquè s’ha subjectat l’estructura (metàl·lica) de forma matussera a les voltes. Les vibracions poden haver produït “fatiga” als materials, o s’ha produït un nou estat de càrregues no previst (càrrega puntual), que finalment ha originat alguna esquerda a la volta que havia estat “sana” anteriorment.

Conclusió

• Constatem l’excel·lència funcional (i estètica) de les voltes a la catalana per a resoldre les escales dels edificis, pel seu bon comportament estructural tant pel que fa als límits de ruptura com de servei.
• L’enemic de les voltes a la catalana a les escales, l’hem d’anar a buscar sobretot en el desplaçament en sentit horitzontal de les parets de suport de les caixes de les escales. Les voltes a la catalana són molt sensibles als desplaçaments dels seus punts de recolzament en les parets.
• Entenem i sabem que la fàbrica ceràmica té una capacitat de treball a tracció molt superior al que se suposava fins ara, segons l’orientació de les esteses respecta a la força de tracció.
• En aquest sentit, pel que fa a la capacitat de treball a tracció de la fàbrica ceràmica, el CTE no contempla més que uns casos determinats que cal tenir en compte de cara a evitar patologies recurrents en les parets de distribució i de tancament dels edificis, normalment no estructurals.
• De cara a les ITE i en general a qualsevol inspecció tècnica, cal evitar alarmes innecessàries en revisar voltes d’escala a la catalana, abans no s’hagi fet un estudi acurat de les patologies detectades i haver “fet números”, la qual cosa requereix la col·laboració d’un tècnic en estructures experimentat.
• I finalment, he proposat, per si ajudava, un protocol d’actuació de cara a resoldre les patologies en les voltes a la catalana, quan s’hagi pogut verificar l’estabilitat del sistema des d’un punt de vista analític.

Autoria de l’article