Al llarg de la història s’ha pogut comprovar que teories antigues ja superades s’han revitalitzat amb l’aparició de noves eines o nous procediments. Això és el que està passant, ara mateix, amb l’estàtica gràfica. Al mateix temps, actualment, aquesta es troba absolutament abandonada, tant des del punt de vista acadèmic com del professional. Efectivament, no es poden resoldre problemes estructurals amb l’ajuda d’una esquadra i un cartabó, ni tan sols amb un sistema de dibuix automatitzat, quan la modificació de la longitud d’una barra o l’alteració d’una càrrega implica repetir el dibuix des del principi. Però l’aparició de programes de geometria dinàmica ha proporcionat l’eina adequada, i en el moment precís, per donar a l’estàtica gràfica un nou impuls i permetre, no només, resoldre els problemes que planteja l’estàtica gràfica amb relativa facilitat, sinó també situar-se en un context geomètric extraordinàriament interessant i didàctic.
Mirem els següents exemples
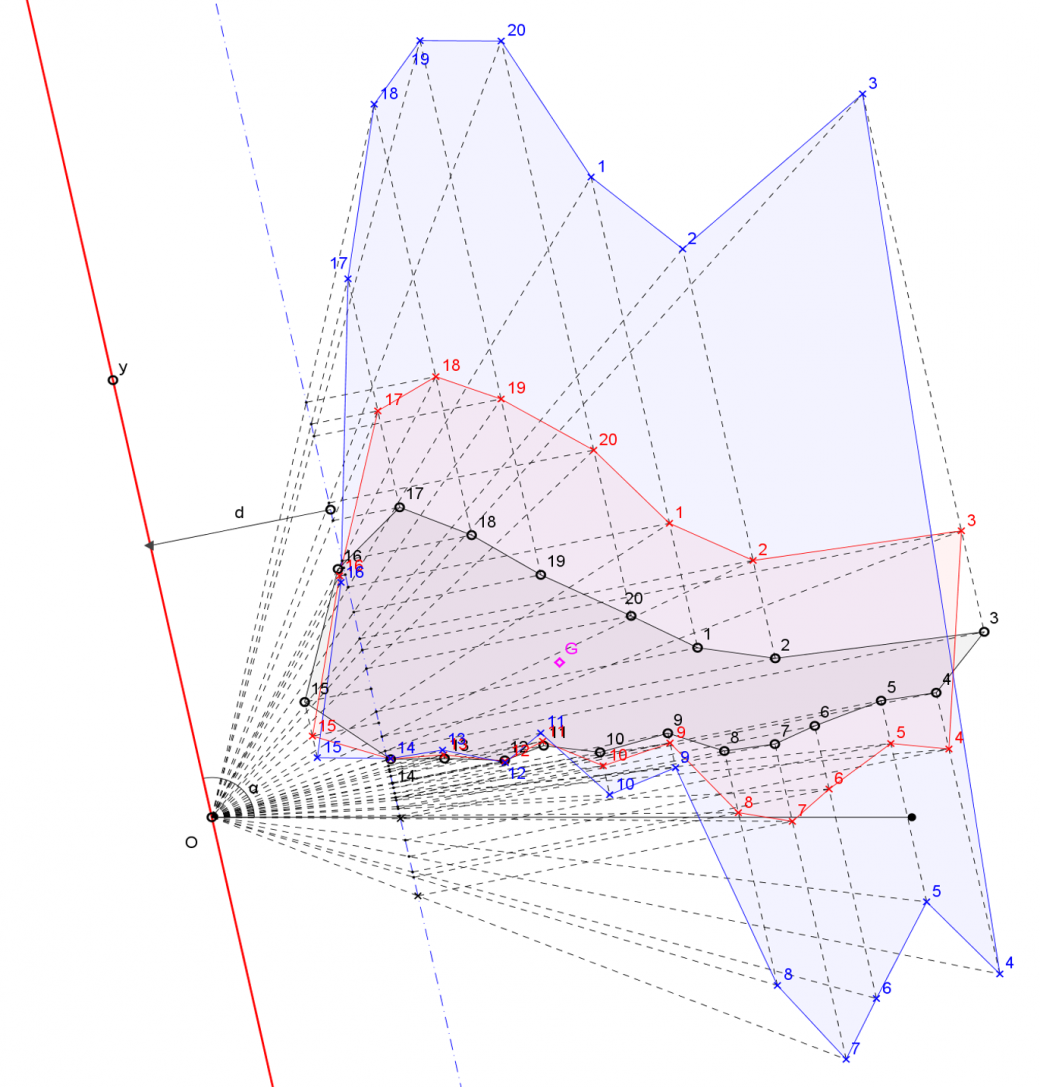
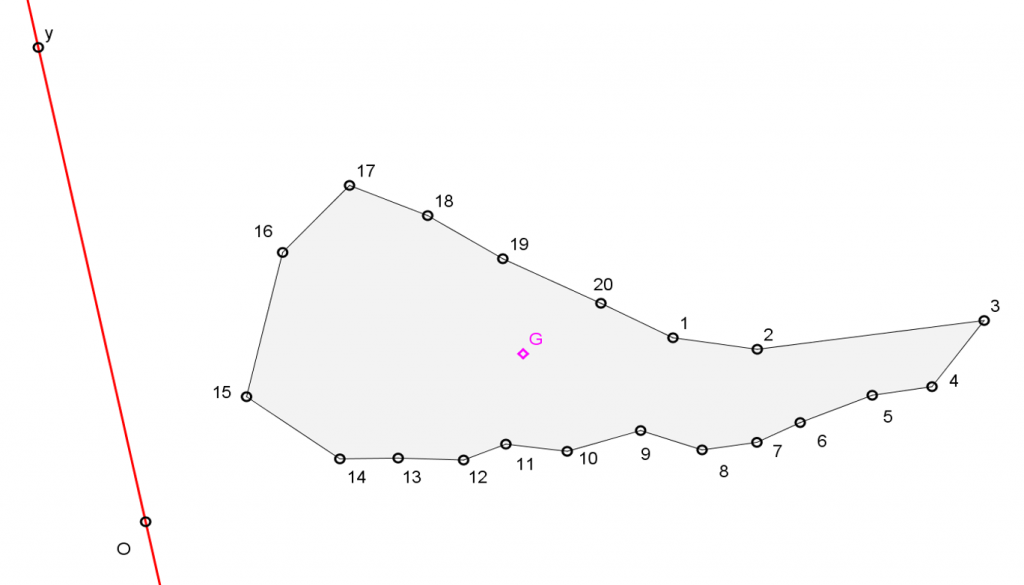
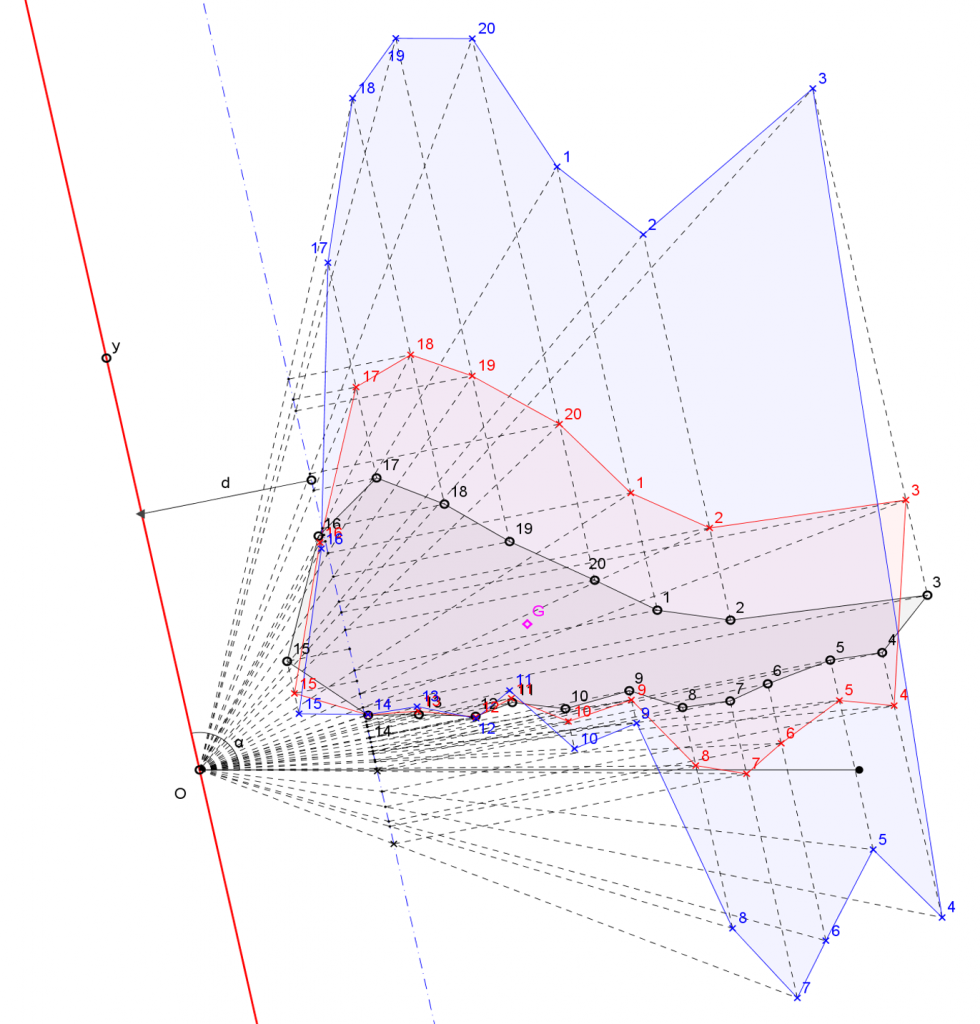
El primer consisteix a calcular un moment estàtic i moment d’inèrcia d’una figura qualsevol amb referència a un eix qualsevol (fig. 1) (1). La figura queda definida per 20 punts que es poden moure amb el ratolí de l’ordinador i, de la mateixa manera, l’eix. Naturalment, tots els moviments filtrats per una escala de longituds. La construcció donada per l’estàtica gràfica s’observa a la figura 2 i els resultats a la figura 3. D’aquesta manera el problema queda resolt i es pot utilitzar per a altres figures i altres eixos i, en qualsevol instant, podrem revisar el procés efectuat.
(1) Es tracta del mètode de Nehls. Al contrari dels mètodes gràfics de càlcul de moments de inèrcia de Mohr i Culmann, molt més coneguts, el mètode de Nehls no es basa en el polígon funicular. És un sistema gràfic poc conegut del què no existeix gaire bibliografia. En el llibre ‘Mecánica de la Construcción’ de Ramon Termens Mauri, publicat el 1950 pel mateix autor, es pot trobar una petita referència.
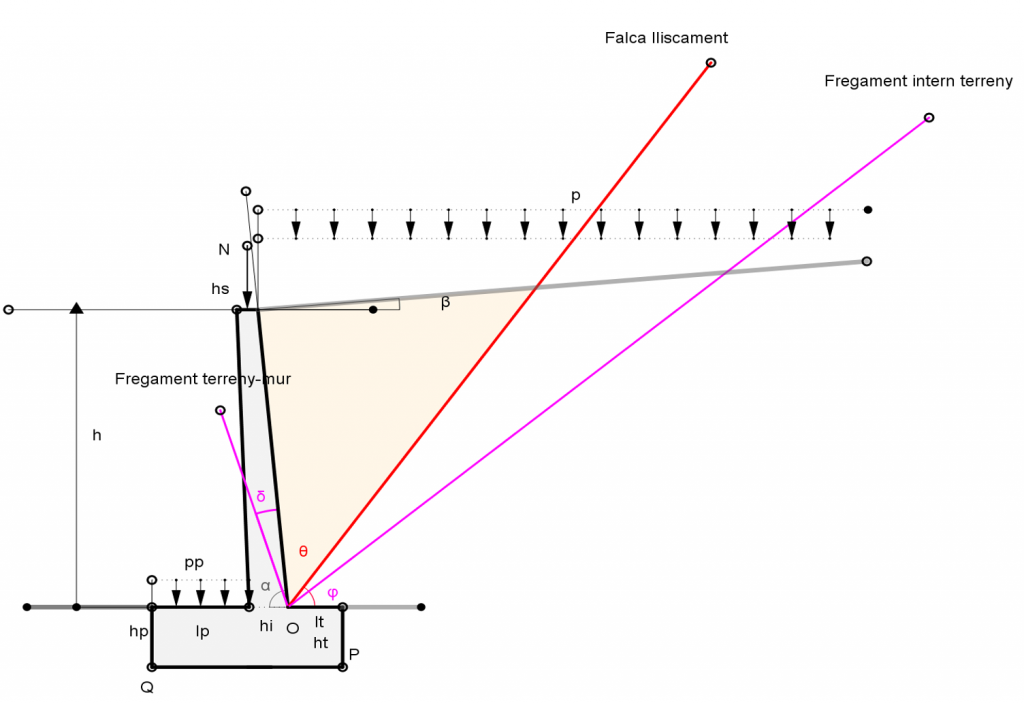
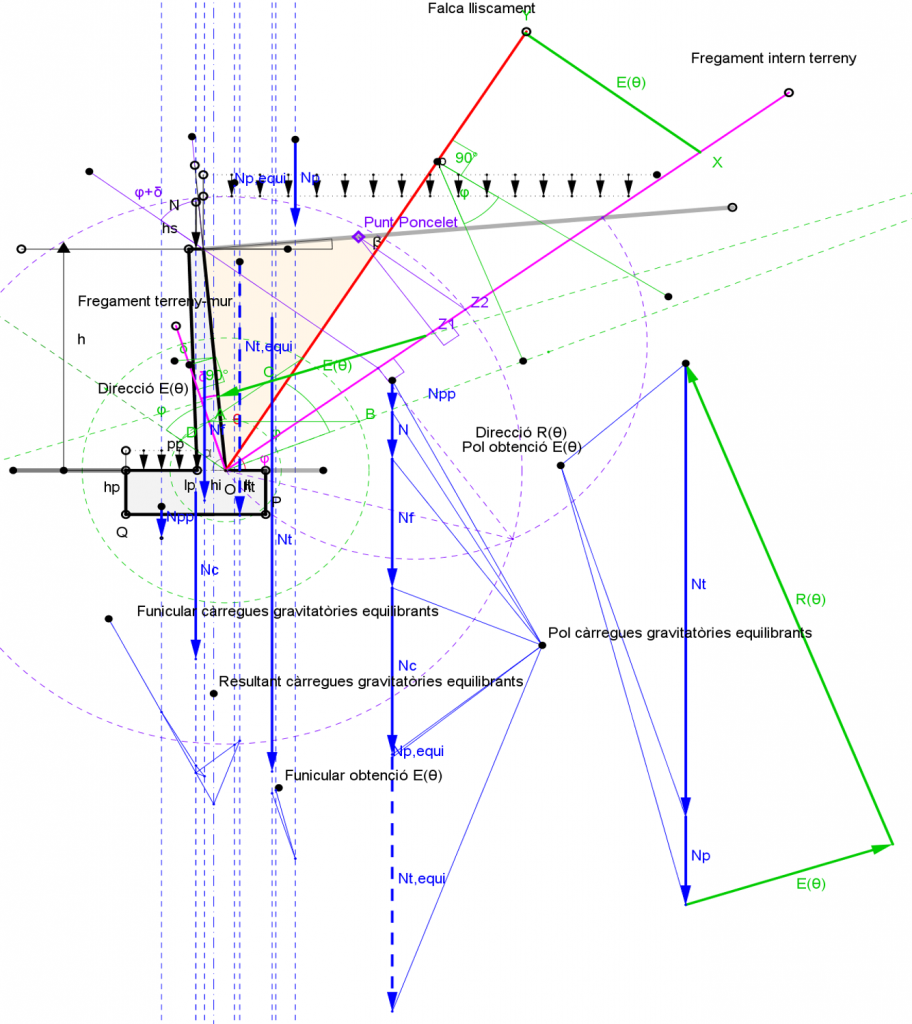
El segon exemple és un mur de contenció de terres. Amb l’ajuda del ratolí de l’ordinador s’introdueixen les característiques geomètriques del mur com l’alçada, les dimensions de la fonamentació, la inclinació i dimensions del fust, forces exteriors, etc. (fig. 4). I amb punts lliscants, les característiques geotècniques del terreny, pes específic del mur, etc. La construcció gràfica està explicada a la figura 5 i, fonamentalment del que es tracta, és d’establir l’equilibri per a cada moviment de la falca de lliscament. La dificultat històrica per determinar els valors dels paràmetres del terreny fa que el mètode gràfic proposat en aquest exemple, que permet moltes hipòtesis amb molt poc esforç, tingui una importància excepcional. Existeixen molts mètodes gràfics per calcular les empentes dels murs en mènsula i han estat molts els autors que ho han estudiat (2). Els valors obtinguts (fig. 6) són la seguretat a la bolcada i les tensions que es produeixen a la fonamentació. Com que el valor de l’empenta és conegut, fàcilment es troben els moments flectors en el fust.
(2) Entre els autors que han estudiat les empentes de les terres destaquen Charles-Augustin de Coulomb (1736-1806) i Jean Poncelet (1788-1867). Ells han desenvolupat sistemes gràfics però també analítics. Observi’s que la intensitat i situació de l’empenta ve en funció de la col·locació de la falca de lliscament. El punt de Poncelet permet col·locar la falca en el punt en què l’empenta es màxima.
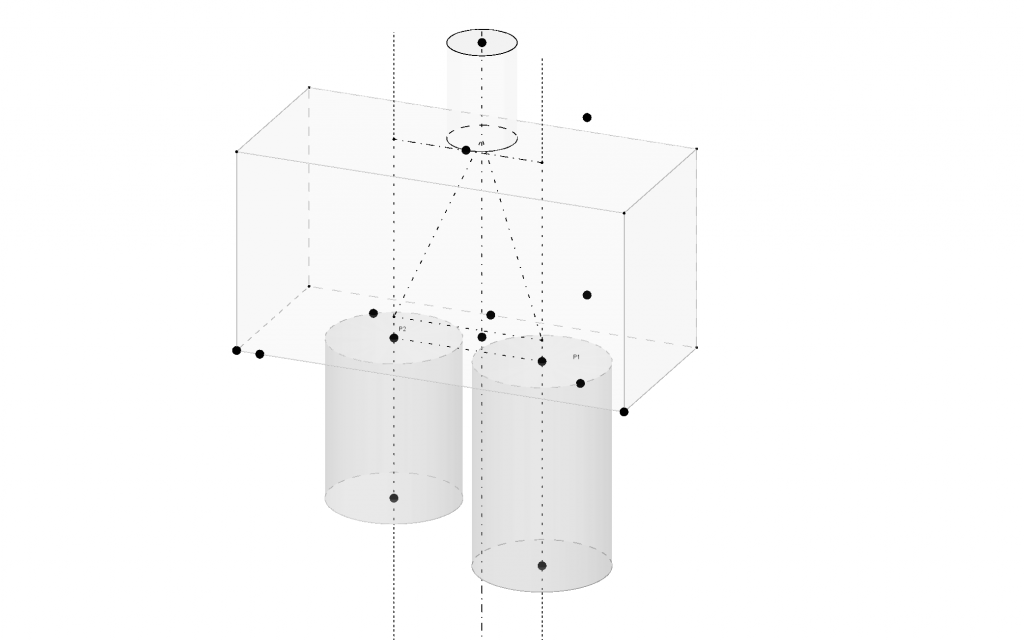
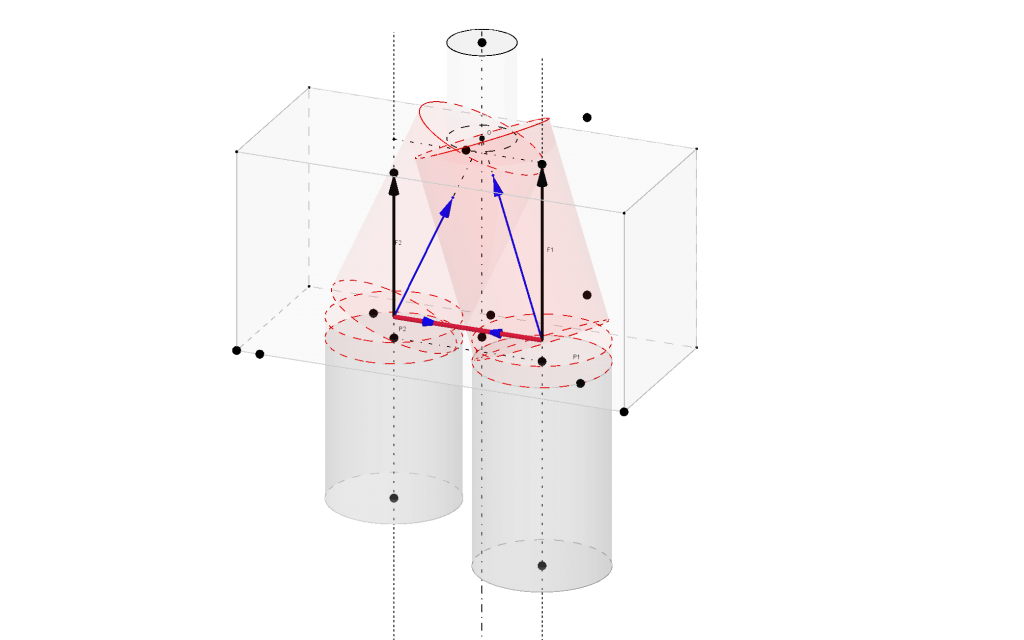
El tercer exemple és un capçal per a dos pilons (fig. 7). En aquest exemple l’estàtica gràfica serveix únicament per descompondre la càrrega que baixa pel suport amb altres dues forces, una a compressió per a les bieles i una a tracció per a l’armadura (fig. 8). Aquí la gràcia d’utilitzar un sistema gràfic consisteix en la facilitat de modificar la geometria del capçal i la disposició dels pilons i observar-ho en 3D (3). En efecte, una primera aproximació consisteix en orientar les bieles i tirants de tal forma que les primeres treballin a compressió i les segones a tracció.
(3) Els capçals sobre dos pilons queden inclosos a les regions D, que són aquelles que no compleixen la teoria general de la flexió. En aquest exemple, l’equilibri s’expressa mitjançant les bieles a compressió i els tirants a tracció. En estructures més complicades es pot pensar en utilitzar mètodes de descomposició de forces com el de Cremona però, en general, serà suficient plantejar l’equilibri amb triangles de forces.
El denominador comú dels tres exemples és el següent:
.1. S’ha aplicat, com sistema per resoldre el problema estructural, l’estàtica gràfica. El més interessant d’aquesta és que, a mesura que es va avançant en el traçat gràfic, també va avançant la resolució del problema.
.2. Es pot seguir el procés de càlcul gràfic i modificar, de forma immediata, el que es cregui convenient per obtenir els resultats desitjats.
.3. El càlcul gràfic es pot realitzar a mà, o d’una forma més sofisticada, amb un sistema automatitzat de dibuix com l’Autocad o similar. En el nostre cas s’ha utilitzat GeoGebra (4).
(4) El programa GeoGebra es deu al matemàtic Marcus Hohenwarter (Salzburg 1976). Va ser la seva tesi doctoral presentada el 2002. Des d’aquesta data el programa ha anat ampliant-se i millorant fins a les versions 5 i 6 actuals. Es tracta d’un programa de software lliure. A la pagina web de GeoGebra el programa pot ser descarregat de forma gratuïta.
El programa de geometria dinàmica GeoGebra, tot i tractar-se d’un programa que no calcula ni dibuixa, és el més adequat per resoldre problemes d’estàtica gràfica. Tot consisteix en què, tant els punts com les rectes o els segments que constitueixen les figures són mòbils, és a dir, es poden moure amb el ratolí de l’ordinador. De forma que cadascun d’aquests moviments implica una situació nova en el procés gràfic. Això vol dir:
.1. Que l’execució d’hipòtesis es converteix en feina molt simple.
.2. Que aquesta simplicitat per a la realització d’hipòtesis fa que la principal virtut del programa GeoGebra sigui la de moure’s en un entorn extraordinàriament didàctic.
L’estàtica gràfica queda sintetitzada en un llibre. És ‘Die graphische Statik’ de Karl Culmann (1821-1881) publicat el 1866. És un moment en què la irrupció del ferrocarril és imparable i és urgent construir ponts per salvar rius i valls i sistemes per poder-los calcular. Tot i que els mètodes analítics ja es coneixien i es podien aplicar, resultava més senzill i operatiu utilitzar els mètodes gràfics. Fins que l’arribada dels ordinadors, amb la seva velocitat de càlcul, va permetre recuperar els mètodes analítics. Tot és molt lògic, però a les escoles tècniques es va deixar progressivament d’ensenyar estàtica gràfica. Actualment, es poden comptar amb els dits d’una mà les universitats on s’ensenya estàtica gràfica. En conseqüència, actualment a les oficines de càlcul d’estructures es desconeixen i, per tant, no s’apliquen, els sistemes gràfics. D’altra banda, els programes integrats i mètodes numèrics permeten resoldre moltes qüestions que desborden l’estàtica gràfica i que són necessaris en el dia a dia d’aquestes oficines. I s’ha de tenir en compte que aspectes com les estructures hiperestàtiques, el formigó pretesat, etc, no estan a l’abast de l’estàtica gràfica.
La meva situació personal és paradoxal. Atesa la meva edat, quan era estudiant, a les escoles relacionades amb la construcció s’impartia estàtica gràfica, especialment el polígon funicular. I amb el mateix procés que enunciàvem anteriorment, es va anar abandonant a canvi dels mètodes analítics. I la utilització d’aquests mètodes ha circumscrit la meva actuació professional. Ara, amb GeoGebra, puc abandonar, dintre del possible, els mètodes analítics i recuperar els sistemes gràfics. Els publico, de manera gratuïta, en forma d’applets a la pàgina web de GeoGebra a www.geogebra.org/u/genes on trobareu gairebé 400 aplicacions, en algun cas acompanyades d’exemples. L’applet permet llegir i operar les aplicacions però no manipular-les o modificar-les.
A la pàgina web www.aceweb/geometria-estructural de l’Associació de Consultors d’Estructures (ACE), trobareu pràcticament les mateixes aplicacions que en els applets però, en aquest cas, es poden baixar, manipular o modificar. Tant en els applets com a les aplicacions, cadascuna d’elles s’acompanya d’un vídeo i d’una memòria amb la intenció d’ensenyar el moviment dels punts en el primer cas i les fonts i altres detalls de càlcul en el segon cas. L’ACE, conscient del que significa aquesta nova incursió a l’estàtica gràfica, ha posat en funcionament el Club GeoGebra, al que poden assistir associats o no, amb l’objectiu de posar en contacte gent interessada simultàniament en l’estàtica gràfica i en GeoGebra. Un tema tractat recentment al club ha estat els arcs, ja siguin concrecionats o amb dovelles. GeoGebra permet, únicament amb l’ajuda del ratolí de l’ordinador, fer moviments dels punts que passen per les línies de pressió, triar la més convenient, en aquest cas la que produeixi menors excentricitats i calcular les tensions, tant normals com tangencials, que es generen. De la mateixa manera que els arcs, poden analitzar-se gràficament, les cúpules, voltes, arcbotants etc.
Encara que existeixen altres programes en què es pot utilitzar l’estàtica gràfica, com per exemple, el Rhinoceros 3D, l’èxit del programa GeoGebra ha estat inqüestionable. 100 milions d’usuaris el fan servir. S’utilitza especialment per ensenyar de forma didàctica qüestions geomètriques. Han aparegut associacions de GeoGebra per tot el món. Aquí a Catalunya, l’Associació Catalana de GeoGebra (ACG) organitza congressos anuals on es poden presentar ponències.
En aquests moments en què es disposa d’eines que permeten recuperar l’estàtica gràfica d’una manera atractiva i engrescadora, la utilització de GeoGebra permetrà el càlcul d’estructures de forma totalment gratificadora.